Quadratic Probing – Explanation with Example
Quadratic Probing is a collision resolution technique used in open addressing. Instead of checking the next index (as in Linear Probing), it probes quadratically increasing indices to reduce clustering.
Formula for Quadratic Probing
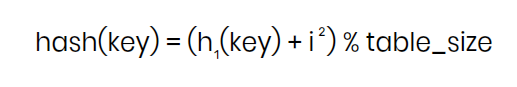
where:
- h1(key) = Primary hash function (
key % table_size) - i = Probe attempt number (starts at 0 and increases: 1, 2, 3, …)
- table_size = Size of the hash table
Example of Quadratic Probing
Given Keys:
101, 203, 309, 412, 512
Hash Table Size:
10
| Key | Hash Code (key % 10) | Stored At Index |
|---|---|---|
| 101 | 101 % 10 = 1 | 1 |
| 203 | 203 % 10 = 3 | 3 |
| 309 | 309 % 10 = 9 | 9 |
| 412 | 412 % 10 = 2 | 2 |
| 512 | 512 % 10 = 2 (Collision!) | Quadratic Probing Used |
Step-by-Step Collision Handling for 512 using Quadratic Probing
- Compute Initial Index using Hash Function
- 512 % 10 = 2
- Index 2 is occupied (by 412) → Collision occurs!
- Apply Quadratic Probing Formula (i² pattern: 1, 4, 9, …)
- i = 1: (2 + 1²) % 10 = (2 + 1) % 10 = 3
- Index 3 is occupied (by 203) → Collision!
- Apply Quadratic Probing Formula Again
- i = 2: (2 + 2²) % 10 = (2 + 4) % 10 = 6
- Index 6 is empty! → Store 512 at index 6
Final Hash Table using Quadratic Probing
| Index | Stored Key(s) |
|---|---|
| 1 | 101 |
| 2 | 412 |
| 3 | 203 |
| 6 | 512 |
| 9 | 309 |
Advantages of Quadratic Probing
✅ Reduces clustering compared to Linear Probing
✅ Efficient for smaller load factors (α < 0.5)
✅ Better performance than Linear Probing in many cases
Load Factor (α) – Explanation
The Load Factor (α) is a measure of how full a hash table is. It helps determine the efficiency of hashing techniques and affects the performance of operations like insertion, search, and deletion.
Formula for Load Factor
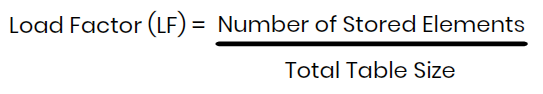
where:
- Number of stored elements = Total number of keys inserted into the table
- Table size = Total number of available slots in the hash table
Example Calculation
Let’s use the following hash table:
| Index | Stored Key(s) |
|---|---|
| 1 | 101 |
| 2 | 412 |
| 3 | 203 |
| 6 | 512 |
| 9 | 309 |
- Number of stored elements = 5 (101, 203, 309, 412, 512)
- Table size = 10
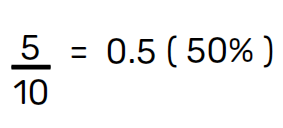
So, the load factor (α) = 0.5
Why is Load Factor Important?
- Low α (< 0.5): Hash table has enough empty spaces, reducing collisions.
- High α (> 0.7): Table is too full, leading to frequent collisions and poor performance.
- Very High α (~1): Almost full table → No available slots → Rehashing needed (increase table size).
🔹 For Open Addressing techniques (like Linear & Quadratic Probing), α < 0.5 is ideal.
🔹 For Chaining, α can be >1 (because each index can store multiple values in a linked list).
How Load Factor Affects Performance
✅ Low α: Faster insert, search, and delete operations (fewer collisions).
❌ High α: More collisions → Increased probing time → Decreased efficiency.
