Priority Queue – Priority Queue C++ – Priority Queue in Data Structure – Coding With Clicks

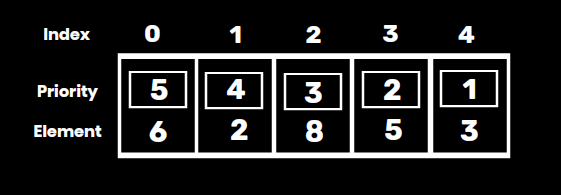
A Priority Queue is a special type of queue in which elements are arranged based on their priority. Unlike a regular queue where elements are served in a first-in-first-out (FIFO) order, a priority queue processes elements according to their priority value. Higher-priority elements are dequeued before lower-priority ones, regardless of their arrival order.

Key Features of a Priority Queue:

1. Priority-Based Ordering: Each element in the queue is associated with a priority. The element with the highest priority (or lowest, depending on implementation) is dequeued first.
2. Dynamic Priority: Priority values can be assigned dynamically (changeable after insertion) or predetermined (fixed at insertion)
3. Structure: Internally, priority queues are often implemented using data structures like heaps, binary trees, or arrays.

Operations in a Priority Queue:

1. Insertion: Add an element to the queue with an associated priority.
2. Deletion: Remove the element with the highest priority.
3. Peek (or Front): Retrieve the element with the highest priority without removing it.

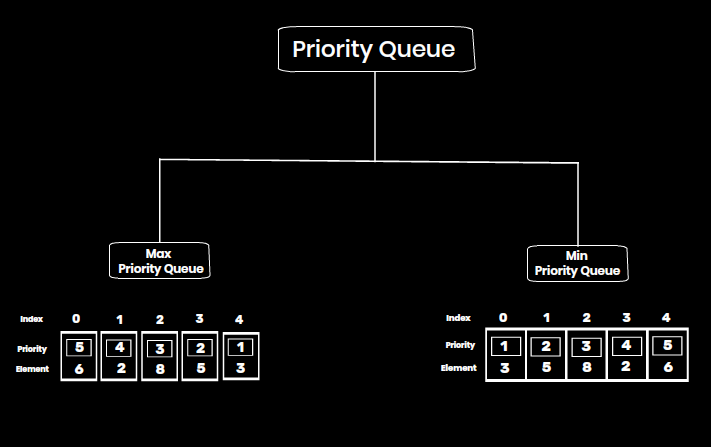
Types of Priority Queue:

1. Max-Priority Queue: The element with the highest priority is served first.
2. Min-Priority Queue: The element with the lowest priority is served first.

Implementation:

• Using Arrays/Linked Lists: Simple to implement but less efficient, as insertion or deletion might require linear time.
• Using Binary Heaps: Commonly used due to their logarithmic time complexity for both insertion and deletion.

Example:

Suppose tasks in an operating system are scheduled using a priority queue:

• Task A (Priority: 3)
• Task B (Priority: 1)
• Task C (Priority: 2)

If implemented as a max-priority queue:

• The tasks will execute in the order: A (3), C (2), B (1).

If implemented as a min-priority queue:

• The tasks will execute in the order: B (1), C (2), A (3).

Here is a C++ implementation of a Priority Queue using an array. In this implementation, higher priority elements are inserted first, and the queue follows the priority order when removing element.

#include <iostream>
using namespace std;
int Data[5], Priority[5];  
int n = 5, s = 0;
void Insert() 
{
    if (s == n) 
    {
        cout << "Queue is full" << endl;
        return;
    }
    int x, p;
    cout << "Enter the element: ";
    cin >> x;
    cout << "Enter its priority: ";
    cin >> p;
    int i = s - 1;
    while (i >= 0 && Priority[i] < p) 
    {
        Data[i + 1] = Data[i];
        Priority[i + 1] = Priority[i];
        i--;
    }
    Data[i + 1] = x;          
    Priority[i + 1] = p;
    s++;
}
void Delete() 
{
    if (s == 0) 
    {
        cout << "Queue is empty" << endl;
        return;
    }
    cout << "Element with highest priority (" << Data[0] << ") removed" << endl;
    for (int i = 0; i < s - 1; i++) 
    {
        Data[i] = Data[i + 1];
        Priority[i] = Priority[i + 1];
    }
    s--;
}
void Peek() 
{
    if (s == 0) 
    {
        cout << "Queue is empty" << endl;
    } 
    else 
    {
        cout << "Element with highest priority is: " << Data[0] << endl;
    }
}
void Display() 
{
    if (s == 0) 
    {
        cout << "Queue is empty" << endl;
        return;
    }
    cout << "Queue elements (from highest to lowest priority):" << endl;
    for (int i = 0; i < s; i++) 
    {
        cout << Data[i] << " (Priority: " << Priority[i] << ")" << endl;
    }
}
int main() 
{
    Insert();
    Insert();
    Insert();
    Insert();
    Insert();
    Display();
    Delete();
    Display();
    Peek();
    return 0;
}

Explanation:

1. Array Representation:

• We have two arrays:
  • Data[] stores the elements (data).
  • Priority[] stores the priorities of the corresponding elements.
• These arrays are kept in sync so that the element at index i in Data[] has the priority at index i in Priority[].

2. Insert function:

• This function inserts an element at the correct position based on its priority.
• We iterate through the queue and shift elements with lower priority to the right, making space for the new element in the correct position.

3. Delete function:

• Removes the element with the highest priority (the first element) and shifts the remaining elements to the left.

4. Peek function:

• Displays the element with the highest priority without removing it (i.e., the first element).

5. Display function:

• Displays all elements in the queue, ordered by priority from highest to lowest

Example:

Input:

Enter the element: 5
Enter its priority: 2
Enter the element: 3
Enter its priority: 1
Enter the element: 8
Enter its priority: 3
Enter the element: 2
Enter its priority: 4
Enter the element: 6
Enter its priority: 5

Output:

Queue elements (from highest to lowest priority):
6 (Priority: 5)
2 (Priority: 4)
8 (Priority: 3)
5 (Priority: 2)
3 (Priority: 1)
Element with highest priority (6) removed
Queue elements (from highest to lowest priority):
2 (Priority: 4)
8 (Priority: 3)
5 (Priority: 2)
3 (Priority: 1)
Element with highest priority is: 2

Real-World Applications:

1. CPU Scheduling: Processes with higher priority are executed first.
2. Pathfinding Algorithms: Used in Dijkstra’s and A* algorithms.
3. Event Management: Prioritize events in simulations or games.
4. Data Compression: Huffman coding uses priority queues.