Prim’s Algorithm – Minimum Spanning Tree (MST)
Prim’s Algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST).
Key Features of Prim’s Algorithm
✔ Greedy approach – Always picks the smallest edge.
✔ Best for dense graphs – Works efficiently with adjacency matrix representation.
✔ Time Complexity:
- O(V²) with an adjacency matrix.
- O(E log V) with a priority queue (using Min Heap).
✔ Handles disconnected graphs – Can be modified to work for disconnected graphs by applying it to each connected component separately.
Steps of Prim’s Algorithm
1️⃣ Initialize:
- Select any vertex as the starting node.
- Mark it as part of the MST.
2️⃣ Pick the Minimum Edge:
- From the vertices in the MST, choose the edge with the smallest weight that connects to an unvisited vertex.
3️⃣ Add the Chosen Edge to the MST:
- Mark the connected vertex as visited.
4️⃣ Repeat Steps 2 & 3:
- Continue adding edges until all vertices are included in the MST.
- The MST will have V-1 edges, where V is the number of vertices.
5️⃣ Output the MST:
- The selected edges form the Minimum Spanning Tree.
- The sum of these edge weights is the minimum total cost.
Example of Prim’s Algorithm
Graph Representation
Consider the following connected & undirected graph:
| Edge | Weight |
|---|---|
| A — B | 2 |
| A — C | 3 |
| B — C | 1 |
| B — D | 4 |
| C — D | 5 |
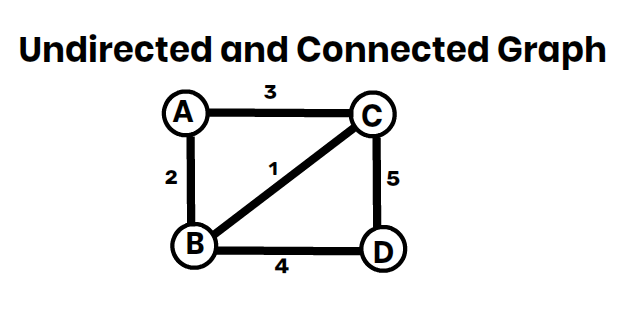
Step 1: Choose a Starting Vertex
- Pick any vertex to start (e.g., A).
- Mark A as part of the MST ✅
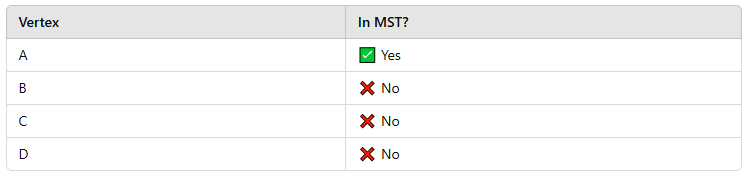
Step 2: Pick the Minimum Edge
- Consider all edges that connect A to unvisited vertices.
- A → B (2)
- A → C (3)
- Smallest edge is A → B (2) → Add it to the MST.

- Vertices connected by edge A-B are A and B. A is already marked as visited and added to the MST.
- Now B is marked as part of the MST.
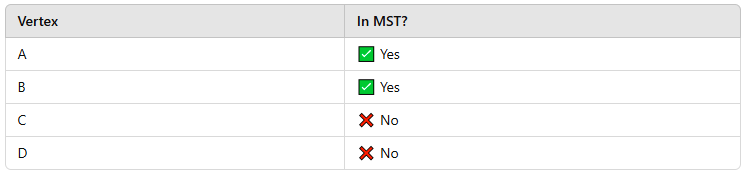
Step 3: Pick the Next Minimum Edge
- Consider all edges that connect the visited vertices (A, B) to unvisited vertices.
- Available edges: A → C (3), B → C (1), B → D (4)
- Smallest edge is B → C (1) → Add it to the MST.

- Vertices connected by edge B-C are B and C. B is already marked as visited and added to the MST.
- Now C is marked as part of the MST.
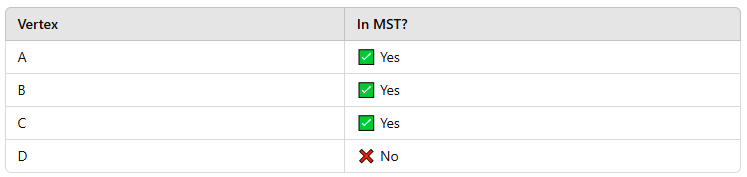
Step 4: Pick the Next Minimum Edge
- Consider all edges that connect the visited vertices (A, B, C) to unvisited vertices.
- Available edges: B → D (4), C → D (5).
- Smallest edge is B → D (4) → Add it to the MST.

- Vertices connected by edge B-D are B and D. B is already marked as visited and added to the MST.
- Now D is marked as part of the MST.
Step 4: Output the MST
✅ Final MST Edges:
1️⃣ A — B (2)
2️⃣ B — C (1)
3️⃣ B — D (4)
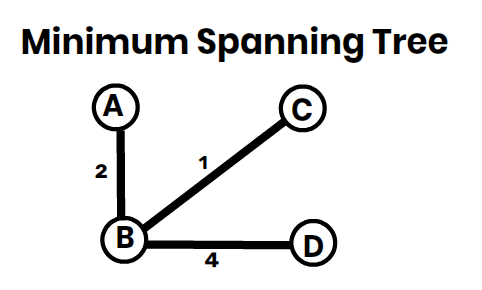
✅ Total Cost of MST = 2 + 1 + 4 = 7
Prim’s Algorithm vs. Kruskal’s Algorithm
| Feature | Prim’s Algorithm | Kruskal’s Algorithm |
|---|---|---|
| Approach | Greedy | Greedy |
| Data Structure | Priority Queue (Heap) | Disjoint Set (Union-Find) |
| Best for | Dense Graphs (Matrix) | Sparse Graphs (Edge List) |
| Time Complexity | O(V²) (Adj. Matrix), O(E log V) (Heap) | O(E log E) (Sorting Edges) |
| Graph Type | Undirected, Weighted, Connected | Undirected, Weighted, Connected, Disconnected (Modified) |
| Cycle Detection | No explicit check | Uses Union-Find |
