Kruskal’s Algorithm (Minimum Spanning Tree – MST)
Kruskal’s Algorithm is a greedy algorithm used to find the Minimum Spanning Tree (MST).

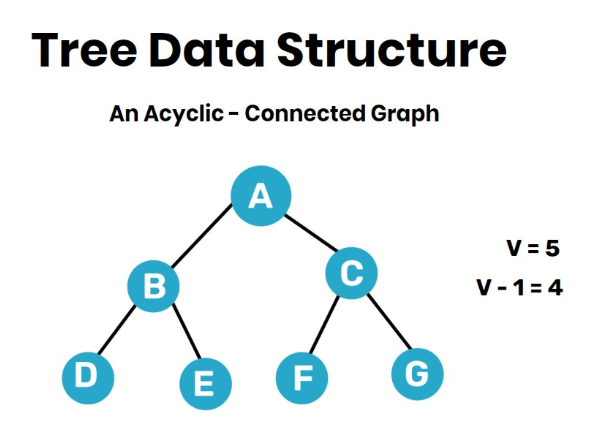
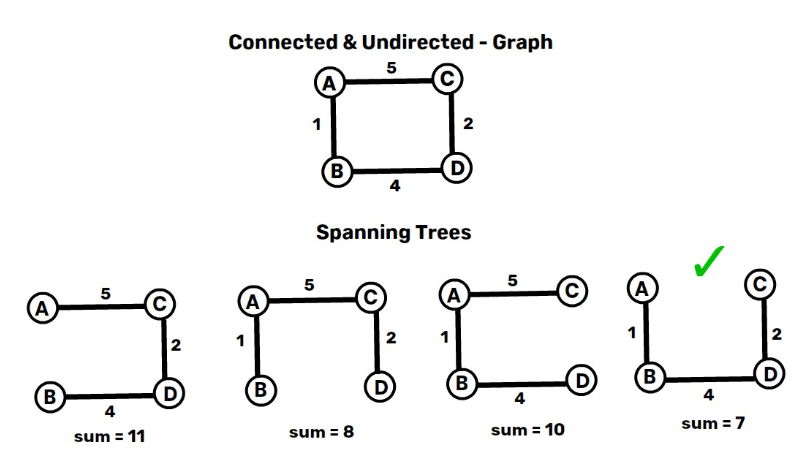
Spanning Trees & Minimum Spanning Tree Example
Key Features of Kruskal’s Algorithm
✔ Greedy approach – Always picks the smallest available edge.
✔ Works for both sparse and dense graphs.
✔ Uses Union-Find (Disjoint Set) to detect cycles.
✔ Best suited for edge list representation of graphs.
✔ Does not work for disconnected graphs (unless modified).

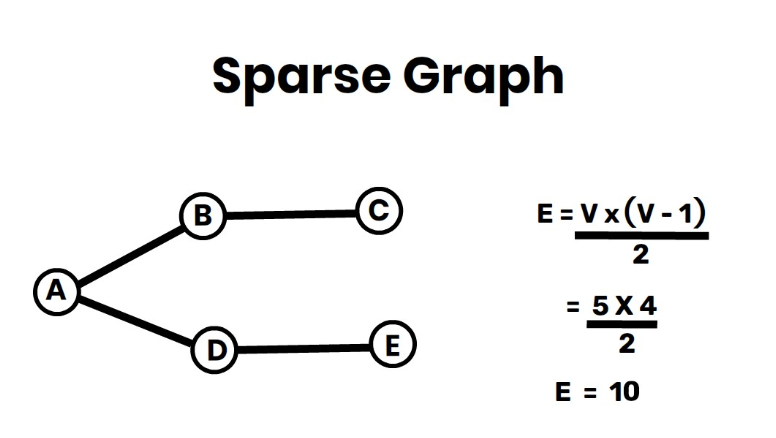
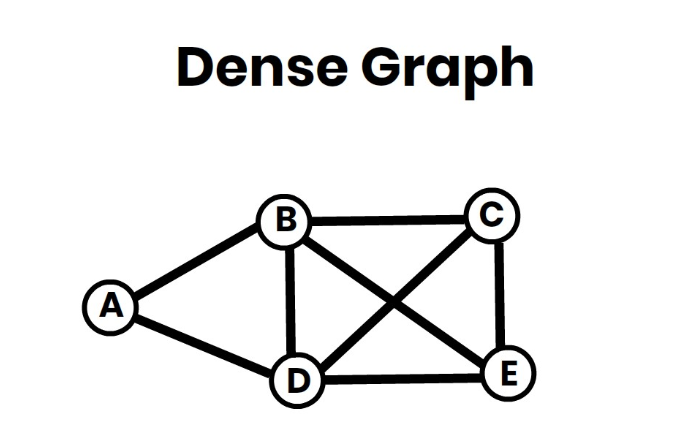

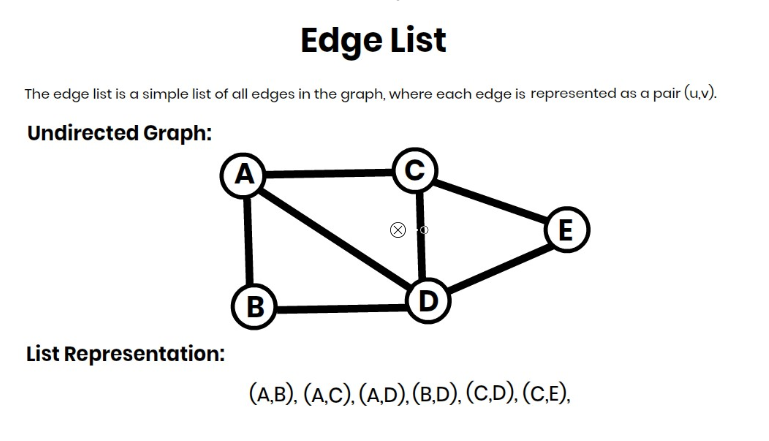
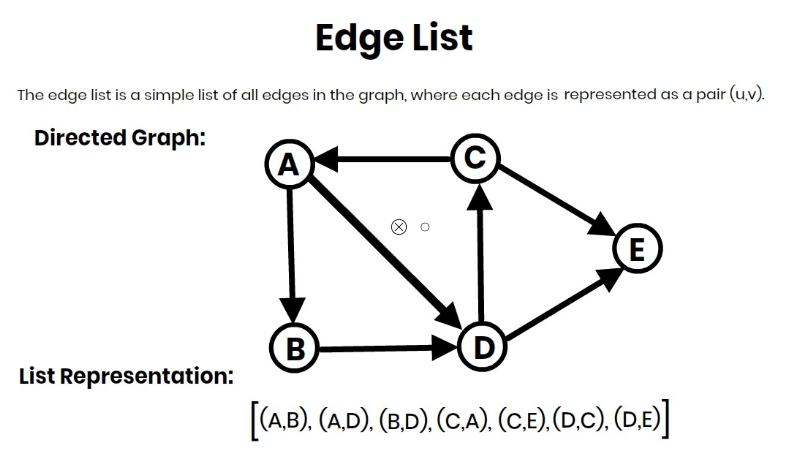
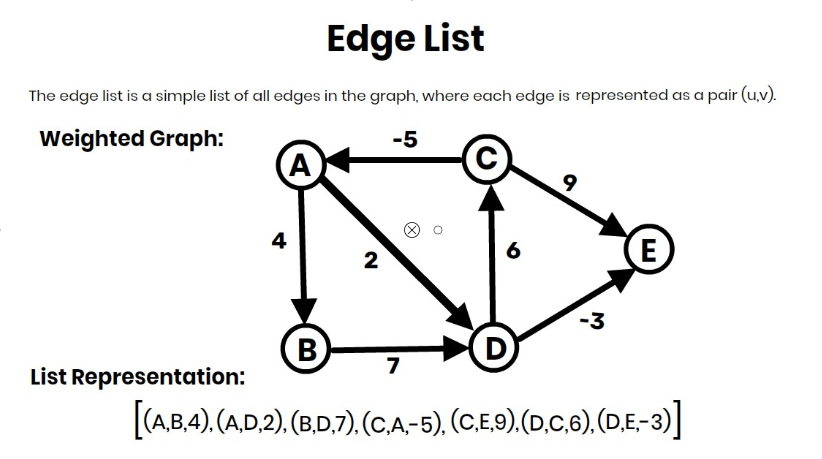
Time Complexity of Kruskal’s Algorithm
- Sorting edges: O (E log E)
- Finding and merging sets (Union-Find): O (E log V)
- Total Complexity: O( E log E) (Since E log E dominates E log V)
Steps of Kruskal’s Algorithm
1️⃣ Sort all edges in ascending order of their weight.
2️⃣ Initialize MST with an empty set (no edges initially).
3️⃣ Pick the smallest edge:
- If adding this edge does not create a cycle, add it to the MST.
- Otherwise, discard the edge.
4️⃣ Repeat until MST contains (V-1) edges, where V is the number of vertices.
5️⃣ Output the MST and its total weight.
Example: Kruskal’s Algorithm Step-by-Step
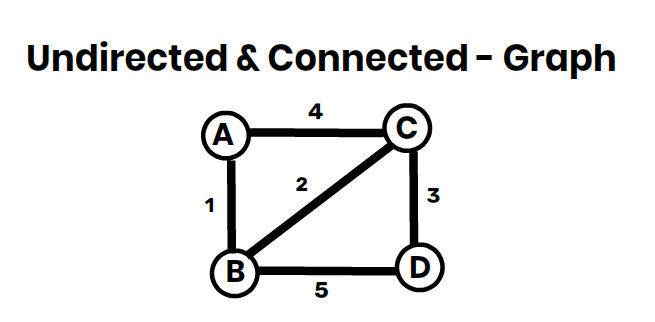
Graph Representation (Edges & Weights)
Consider the following undirected & connected graph:
| Edge | Weight |
|---|---|
| A — B | 1 |
| A — C | 4 |
| B — C | 2 |
| B — D | 5 |
| C — D | 3 |
Step 1: Sort Edges in Ascending Order
| Edge | Weight |
|---|---|
| A — B | 1 |
| B — C | 2 |
| C — D | 3 |
| A — C | 4 |
| B — D | 5 |
Step 2: Initialize MST
- Initially, the MST is empty.

Step 3: Pick the Smallest Edges and Check for Cycles
1️⃣ Pick A — B (1) ✅ → Add to MST
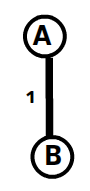

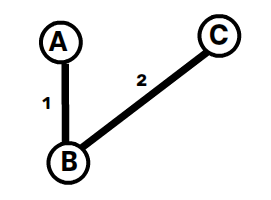
2️⃣ Pick B — C (2) ✅ → Add to MST

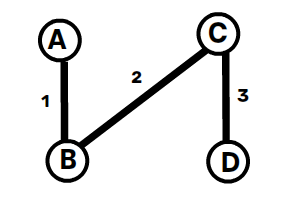
3️⃣ Pick C — D (3) ✅ → Add to MST

Repeat until MST contains (V-1) edges, where V is the number of vertices.” means that we keep adding edges to the Minimum Spanning Tree (MST) until it has exactly (V-1) edges.
🔹 Why (V-1) Edges?
- A Minimum Spanning Tree (MST) is a tree that connects all V vertices with the minimum possible total edge weight.
- A tree with V vertices always has exactly (V-1) edges (This is a fundamental property of trees in graph theory).
- If we add more than (V-1) edges, a cycle will form, and it won’t be a tree anymore.
- If we have fewer than (V-1) edges, the graph will remain disconnected, and it won’t be a spanning tree.
So,
- Now, we have 3 edges in MST (V-1 = 4-1 = 3).
- We STOP because we’ve reached V-1 edges.
- We ignore A — C (4) & B — D (5) because we already have an MST.
But for your understanding, let’s check A — C (4) and B — D (5) as well.
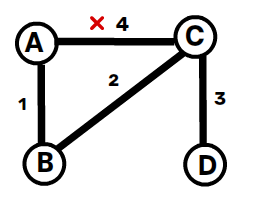
4️⃣ Pick A — C (4) ❌ (Cycle detected, discard)
5️⃣ Pick B — D (5) ❌ (Cycle detected, discard)
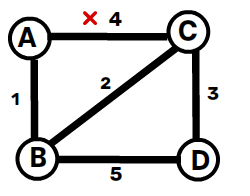
Step 4: Output the MST
Final MST:
| Edge | Weight |
|---|---|
| A — B | 1 |
| B — C | 2 |
| C — D | 3 |
✅ Minimum Spanning Tree Weight = 1 + 2 + 3 = 6
