Floyd Warshall Algorithm – Floyd Warshall Algorithm in Data Structure – Floyd Warshall Algorithm in Graph Theory

Floyd-Warshall Algorithm

The Floyd-Warshall Algorithm is an efficient way to find the shortest paths between all pairs of nodes in a weighted graph. It works for both directed and undirected graphs and can handle negative edge weights (but not negative cycles).

Key Features:

1. All-Pairs Shortest Paths:
   Unlike Dijkstra or Bellman-Ford (which find shortest paths from a single source), Floyd-Warshall finds the shortest paths between every pair of vertices.
2. Dynamic Programming Approach:
   It progressively updates the shortest path between pairs of vertices by considering intermediate nodes.
3. Handles Negative Weights:
   It works with negative edge weights, but if there’s a negative weight cycle, the algorithm can detect it.

Time Complexity:

• O(V³), where V is the number of vertices. This makes it efficient for dense graphs or when we need all-pairs shortest paths.

Algorithm Steps:

1. Initialization:
   • Create a distance matrix dist[][] where dist[i][j] represents the shortest distance from node i to node j.
   • If there’s no direct edge between i and j, set dist[i][j] = ∞ (infinity).
   • For self-loops (distance from a node to itself), set dist[i][i] = 0.
2. Iterative Update:
   For every node k (considered as an intermediate node):
   • Update the shortest distance between nodes i and j by checking if the path i → k → j is shorter than the current i → j.
   Formula: dist[i][j] = min⁡(dist[i][j], dist[i][k]+dist[k][j])
3. Repeat for all nodes k, until no more updates can be made.

Example:

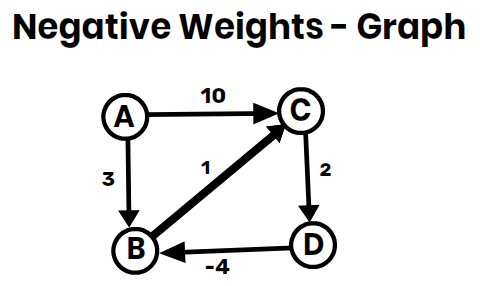
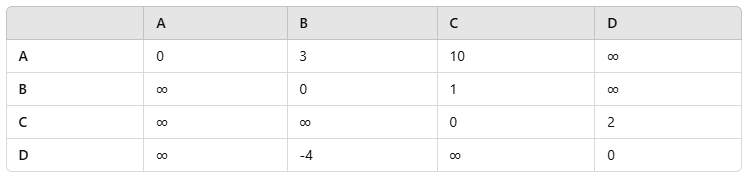
1. Initial Distance Matrix:

2. Update the Matrix Using Intermediate Nodes:

Using A as intermediate: No updates (since A doesn’t reduce any paths).

For each pair (i, j), we check if the path through A is shorter.

Checking all pairs:

From (i)	To (j)	Current dist[i][j]	Via A (dist[i][A] + dist[A][j])	Update?
A	A	0	0 + 0 = 0	No change
A	B	3	0 + 3 = 3	No change
A	C	10	0 + 10 = 10	No change
A	D	∞	0 + ∞ = ∞	No change
B	A	∞	∞ + 0 = ∞	No change
B	B	0	∞ + 3 = ∞	No change
B	C	1	∞ + 10 = ∞	No change
B	D	∞	∞ + ∞ = ∞	No change
C	A	∞	∞ + 0 = ∞	No change
C	B	∞	∞ + 3 = ∞	No change
C	C	0	∞ + 10 = ∞	No change
C	D	2	∞ + ∞ = ∞	No change
D	A	∞	∞ + 0 = ∞	No change
D	B	-4	∞ + 3 = ∞	No change
D	C	∞	∞ + 10 = ∞	No change
D	D	0	∞ + ∞ = ∞	No change

Using B as intermediate:

For each pair (i, j), we check if the path through B is shorter.

Checking all pairs:

From (i)	To (j)	Current dist[i][j]	Via B (dist[i][B] + dist[B][j])	Update?
A	A	0	3 + ∞ = ∞	No change
A	B	3	3 + 0 = 3	No change
A	C	10	3 + 1 = 4	Update (10 → 4) ✅
A	D	∞	3 + ∞ = ∞	No change
B	A	∞	0 + ∞ = ∞	No change
B	B	0	0 + 0 = 0	No change
B	C	1	0 + 1 = 1	No change
B	D	∞	0 + ∞ = ∞	No change
C	A	∞	∞ + ∞ = ∞	No change
C	B	∞	∞ + 0 = ∞	No change
C	C	0	∞ + 1 = ∞	No change
C	D	2	∞ + ∞ = ∞	No change
D	A	∞	-4 + ∞ = ∞	No change
D	B	-4	-4 + 0 = -4	No change
D	C	∞	-4 + 1 = -3	Update (∞ → -3) ✅
D	D	0	-4 + ∞ = ∞	No change

Updated Distance Matrix After Using B as Intermediate

From (i) → To (j)	A	B	C	D
A →	0	3	4	∞
B →	∞	0	1	∞
C →	∞	∞	0	2
D →	∞	-4	-3	0

Using C as intermediate:

For each pair (i, j), we check if the path through C is shorter.

Checking all pairs:

Pair (i → j)	Current Distance	Via C (dist[i][C] + dist[C][j])	Updated?
A → A	0	4+∞=∞4 + ∞ = ∞4+∞=∞	❌ No update
A → B	3	4+∞=∞4 + ∞ = ∞4+∞=∞	❌ No update
A → C	4	4+0=44 + 0 = 44+0=4	❌ No update
A → D	∞	4+2=64 + 2 = 64+2=6	✅ Update to 6
B → A	∞	1+∞=∞1 + ∞ = ∞1+∞=∞	❌ No update
B → B	0	1+∞=∞1 + ∞ = ∞1+∞=∞	❌ No update
B → C	1	1+0=11 + 0 = 11+0=1	❌ No update
B → D	∞	1+2=31 + 2 = 31+2=3	✅ Update to 3
C → A	∞	0+∞=∞0 + ∞ = ∞0+∞=∞	❌ No update
C → B	∞	0+∞=∞0 + ∞ = ∞0+∞=∞	❌ No update
C → C	0	0+0=00 + 0 = 00+0=0	❌ No update
C → D	2	0+2=20 + 2 = 20+2=2	❌ No update
D → A	∞	−3+∞=∞-3 + ∞ = ∞−3+∞=∞	❌ No update
D → B	-4	−3+∞=∞-3 + ∞ = ∞−3+∞=∞	❌ No update
D → C	-3	−3+0=−3-3 + 0 = -3−3+0=−3	❌ No update
D → D	0	−3+2=−1-3 + 2 = -1−3+2=−1	❌ No update

Updated Distance Matrix After Using C as Intermediate

	A	B	C	D
A	0	3	4	6
B	∞	0	1	3
C	∞	∞	0	2
D	∞	-4	-3	0

Using D as intermediate:

For each pair (i, j), we check if the path through D is shorter.

Checking all pairs:

Pair (i → j)	Current Distance	Via D (dist[i][D] + dist[D][j])	Updated?
A → A	0	6+∞=∞6 + ∞ = ∞6+∞=∞	❌ No update
A → B	3	6+(−4)=26 + (-4) = 26+(−4)=2	✅ Update to 2
A → C	4	6+(−3)=36 + (-3) = 36+(−3)=3	✅ Update to 3
A → D	6	6+0=66 + 0 = 66+0=6	❌ No update
B → A	∞	3+∞=∞3 + ∞ = ∞3+∞=∞	❌ No update
B → B	0	3+(−4)=−13 + (-4) = -13+(−4)=−1	✅ Update to -1
B → C	1	3+(−3)=03 + (-3) = 03+(−3)=0	✅ Update to 0
B → D	3	3+0=33 + 0 = 33+0=3	❌ No update
C → A	∞	2+∞=∞2 + ∞ = ∞2+∞=∞	❌ No update
C → B	∞	2+(−4)=−22 + (-4) = -22+(−4)=−2	✅ Update to -2
C → C	0	2+(−3)=−12 + (-3) = -12+(−3)=−1	✅ Update to -1
C → D	2	2+0=22 + 0 = 22+0=2	❌ No update
D → A	∞	0+∞=∞0 + ∞ = ∞0+∞=∞	❌ No update
D → B	-4	0+(−4)=−40 + (-4) = -40+(−4)=−4	❌ No update
D → C	-3	0+(−3)=−30 + (-3) = -30+(−3)=−3	❌ No update
D → D	0	0+0=00 + 0 = 00+0=0	❌ No update

Updated Distance Matrix After Using D as an Intermediate

	A	B	C	D
A	0	2	3	6
B	∞	-1	0	3
C	∞	-2	-1	2
D	∞	-4	-3	0

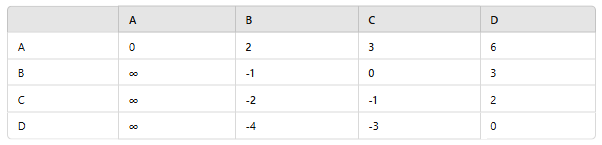
3. Final Distance Matrix (All-Pairs Shortest Paths):

Detecting Negative Cycles:

To check if a negative weight cycle exists in the graph, we need to look at the diagonal elements of the final distance matrix.

• If dist[i][i] < 0 for any node i, it means there’s a negative weight cycle.

Checking Diagonal Elements:

• dist[A][A] = 0
• dist[B][B] = -1
• dist[C][C] = -1
• dist[D][D] = 0

The graph contains a negative weight cycle because dist[B][B] < 0 and dist[C][C] < 0.

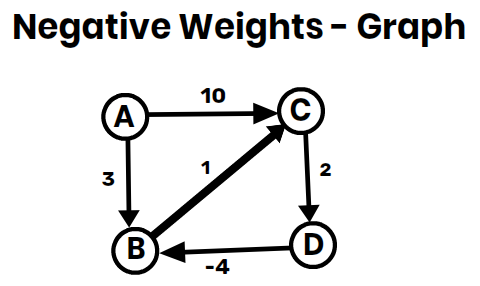
Negative weight cycle: B -> C -> D -> B

Note:

For V = 4 (A, B, C, D):

• There are 4×4=16 (i, j) pairs.
• We check all 16 pairs for each intermediate node (A, B, C, D).
• This results in 4×16=64 checks.