Dijkstra Algorithm in Data Structure – Dijkstra Algorithm Shortest Path – Dijkstra Algorithm Example

Dijkstra’s algorithm finds the shortest path from a source vertex to all other vertices in a weighted graph with non-negative edge weights.

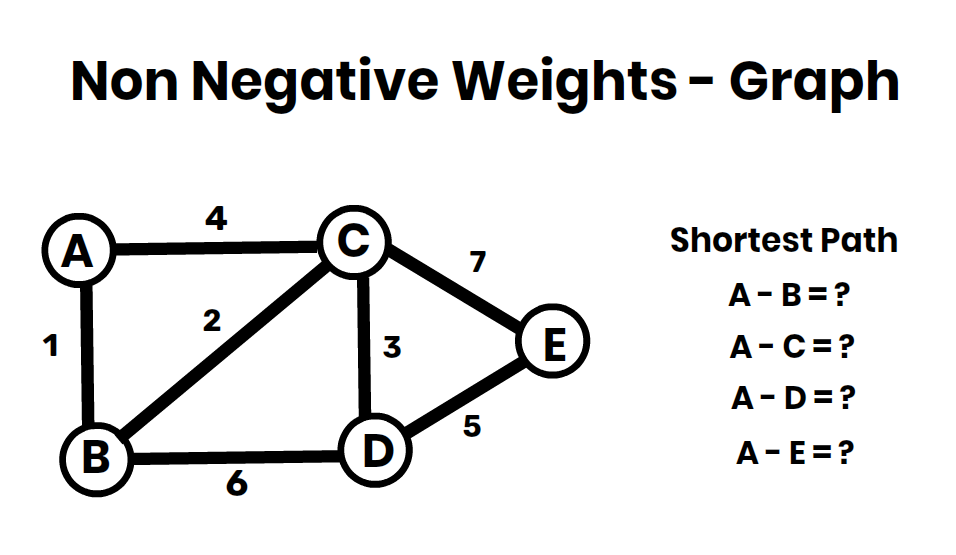
Steps of the Algorithm

1. Initialization:
   • Assign a tentative distance of 0 to the starting node (source) and infinity to all other nodes.
   • Mark all nodes as unvisited. The starting node is considered as the “current node.”
2. Updating Neighbors:
   • For the current node, examine all its unvisited neighbors.
   • Calculate the tentative distance to each neighbor as: Tentative Distance=Current Node’s Distance + Edge Weight to Neighbor
   • If this tentative distance is smaller than the current recorded distance for that neighbor, update it.
3. Mark as Visited:
   • Once all neighbors of the current node are considered, mark the current node as visited. Visited nodes are not revisited.
4. Select Next Node:
   • From the unvisited nodes, select the node with the smallest tentative distance as the next “current node.”
5. Repeat:
   • Repeat steps 2–4 until all nodes are visited or the smallest tentative distance among the unvisited nodes is infinity (indicating unreachable nodes).
6. Result:
   • The shortest distance from the source node to each node is now determined.

Steps

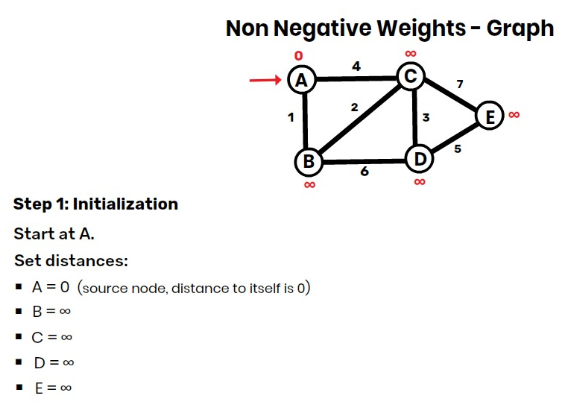
Step 1: Initialization

Start at A.
Set distances:

• A=0 (source node, distance to itself is 0)
• B=∞
• C=∞
• D=∞
• E=∞

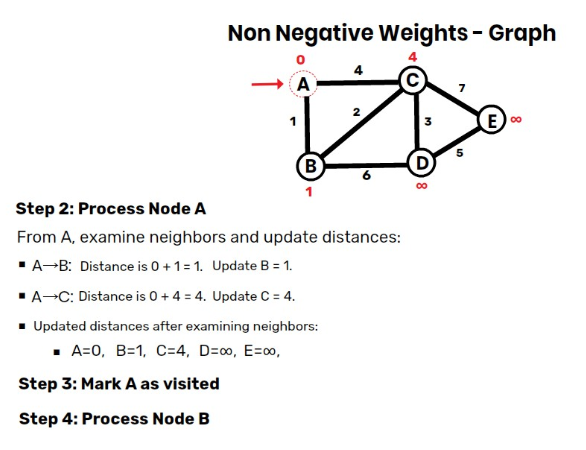
Step 2: Process Node AAA

From A, examine neighbors and update distances:

• A→B: Distance is 0+1=1. Update B=1.
• A→C: Distance is 0 + 4 = 4 Update C=4.

Updated distances after examining neighbors:

• A=0,B=1,C=4,D=∞,E=∞.

Mark A as visited.

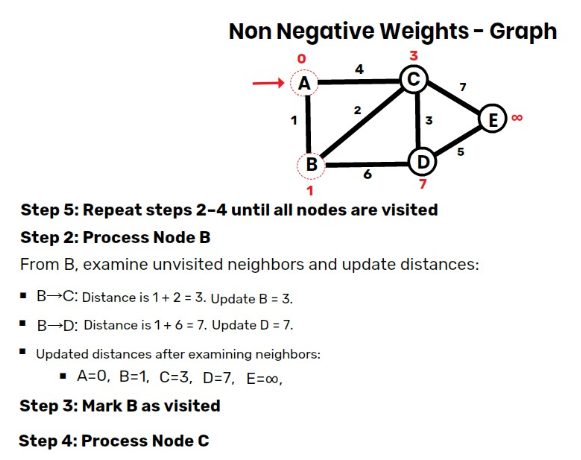
Step 3: Process Node B (Unvisited Node with Smallest Distance)

From BBB, examine neighbors and update distances:

• B→C: Distance is 1+2=3. Update C=3 (shorter than previous 4).
• B→D: Distance is 1+6=7. Update D=7.
• Updated distances:
  • A=0,B=1,C=3,D=7,E=∞.
• Mark B as visited.

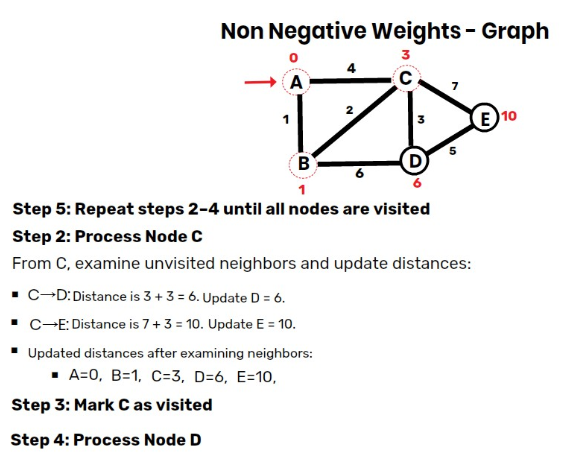
Step 4: Process Node C (Unvisited Node with Smallest Distance)

From C, examine neighbors and update distances:

• C→D: Distance is 3+3=6. Update D=6 (shorter than previous 7).
• C→E: Distance is 3+7=10. Update E=10.
• Updated distances:
  • A=0,B=1,C=3,D=6,E=10.
• Mark C as visited.

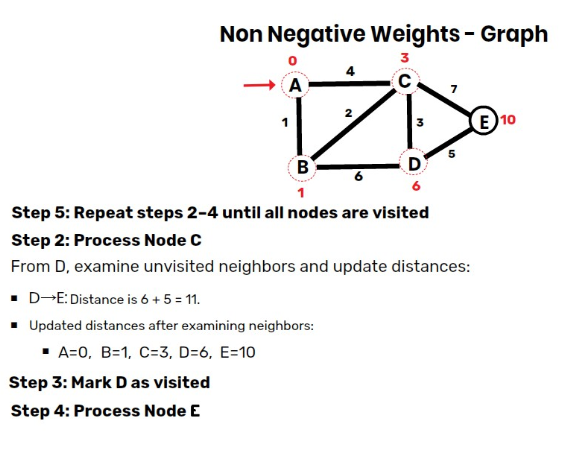
Step 5: Process Node D (Unvisited Node with Smallest Distance)

From D, examine neighbors and update distances:

• D→E: Distance is 6+5=11. No update since E=10 (shorter distance already exists).
• Updated distances:
  • A=0,B=1,C=3,D=6,E=10.
• Mark D as visited.

Step 6: Process Node E

• No neighbors to update.
• Mark E as visited.

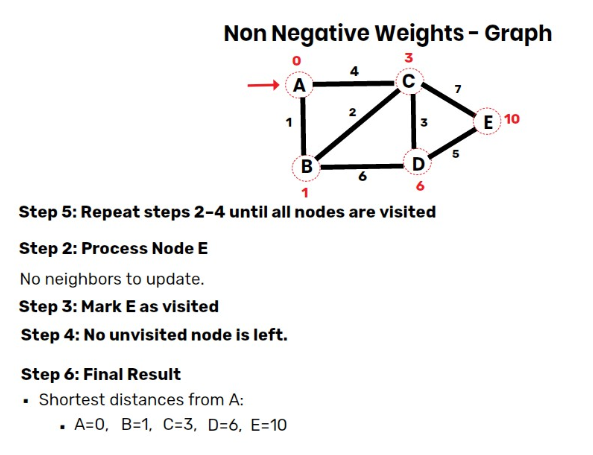
Final Result:

• Shortest distances from A:
  • A=0,B=1,C=3,D=6,E=10.

Path Interpretation:

• Shortest path from A to B: A→B, cost 1.
• Shortest path from A to C: A→C, cost 3.
• Shortest path from A to D: A→D, cost 6.
• Shortest path from A to E: A→E, cost 10.