Collision Resolution Techniques in Hashing

When two keys hash to the same index in a hash table, a collision occurs. To handle collisions, we use collision resolution techniques. There are two main categories:

Separate Chaining (Open Hashing)
Open Addressing (Closed Hashing)

Open Addressing (Closed Hashing)

In this approach, all elements are stored within the hash table itself. If a collision occurs, the algorithm searches for another available slot using a probing sequence.

✔ Types of Open Addressing:

Linear Probing: Find the next available slot sequentially.
- Formula: hash(key) = (h(key) + i) % table_size
- Problem: Clustering (many keys get grouped together).
Quadratic Probing: Instead of checking the next immediate slot, check quadratically farther slots.
- Formula: hash(key) = (h(key) + i²) % table_size
- Reduces clustering but may still fail if the table is not large enough.
Double Hashing: Uses a second hash function to determine the step size for probing.
- Formula: hash(key) = (h1(key) + i * h2(key)) % table_size
- Best among open addressing techniques (avoids clustering).

The step size for probing in Double Hashing determines how far we move (or “jump”) when a collision occurs.

How Step Size Works in Double Hashing

In linear probing, the step size is always 1, meaning we check the next slot sequentially.
In quadratic probing, the step size increases quadratically (1, 4, 9, …).
In double hashing, the step size is calculated using a second hash function h2(key)h_2(key)h2(key), making the jumps non-uniform, reducing clustering.

Formula Explanation

hash(key) = (h1(key) + i * h2(key)) % table_size

h1(key) is the primary hash function (first hash result).
h2(key) is the secondary hash function (step size).

The term “quadratically” means that the step size follows a quadratic sequence—the numbers are squared as they increase.

Quadratic Growth Pattern

A quadratic sequence follows this pattern:

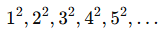
Which results in:

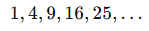
The term “non-uniform” means that the step sizes in double hashing vary and do not follow a fixed pattern like linear or quadratic probing. Instead, the step size depends on a second hash function, making the jumps irregular and reducing clustering.

Probing refers to the process of searching for the next available slot in the hash table when a collision occurs.