Different Problem-Solving Techniques in Programming
Problem-solving in programming involves various techniques to analyze, design, and implement efficient solutions. The most common methods include algorithms, pseudocodes, and flowcharts.
1. Algorithms
An algorithm is a step-by-step procedure or set of rules to solve a specific problem. It defines the logical sequence of operations that must be followed to achieve the desired result.
Types of Algorithm Techniques:
🔹 Brute Force – Try all possible solutions and choose the best one.
🔹 Divide and Conquer – Break the problem into smaller sub-problems, solve them, and combine results (e.g., Merge Sort, Quick Sort).
🔹 Greedy Algorithm – Make the best choice at each step (e.g., Dijkstra’s Algorithm).
🔹 Dynamic Programming – Solve sub-problems and store results to avoid recomputation (e.g., Fibonacci series).
Recomputation means calculating the same value multiple times unnecessarily. In Dynamic Programming, we solve sub-problems and store their results so that we don’t have to compute them again when needed later.
🔹 Backtracking – Try different solutions and backtrack when necessary (e.g., Sudoku Solver, N-Queens Problem).
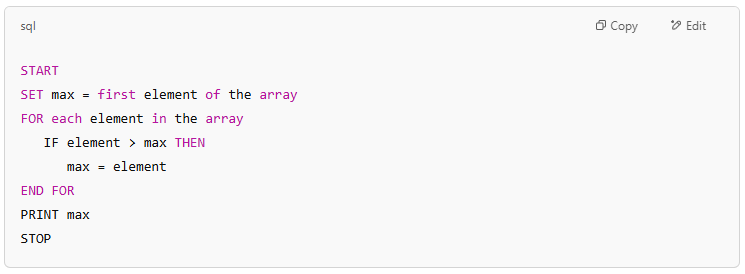
Example Algorithm (Finding the Largest Number in an Array):
- Start
- Initialize a variable max to the first element of the array.
- Loop through the array and compare each element with max.
- If an element is greater than max, update max.
- After the loop ends, max holds the largest value.
- Print max and stop.
2. Pseudocode
Pseudocode is a simplified, informal way of writing algorithms using plain English and basic programming constructs. It helps programmers design solutions before actual coding.
🔹 It does not follow strict syntax like programming languages.
🔹 It focuses on logic rather than implementation details.
Basic Programming Constructs refer to the fundamental building blocks used to write programs. These include:
1️⃣ Sequential Execution – Code runs line by line, in order.
2️⃣ Variables & Data Types – Storing and manipulating values (e.g., numbers, text).
3️⃣ Input/Output – Taking input from users and displaying output.
4️⃣ Decision Making (Selection) – Using conditional statements like if-else and switch to control program flow.
5️⃣ Loops (Iteration) – Using for, while, and do-while loops to repeat tasks.
6️⃣ Functions (Modularity) – Breaking a program into reusable blocks of code.
Pseudocode uses these constructs in plain English, making it easier to plan and understand an algorithm before writing actual code.
Plain English means writing in a simple and easy-to-understand way, without using complex technical terms or difficult language.
For example:
🔹 Technical Language:
“Initialize an integer variable and assign it a value of 5. Subsequently, utilize a loop to iterate until the variable exceeds 10, incrementing its value by 1 in each iteration.”
🔹 Plain English:
“Start with a number 5. Keep adding 1 to it until it becomes greater than 10.”
In pseudocode, we use plain English to describe the logic of a program without worrying about syntax.
Example Pseudocode (Find the Largest Number in an Array):
3. Flowcharts
A flowchart is a graphical representation of an algorithm. It uses different symbols to visually depict the flow of a program.
Depict means to show, illustrate, or represent something visually.
🔹 Ovals – Represent Start/Stop points.
🔹 Parallelograms – Represent Input/Output operations.
🔹 Rectangles – Represent Processing steps (calculations, assignments).
🔹 Diamonds – Represent Decision-making (if-else conditions).
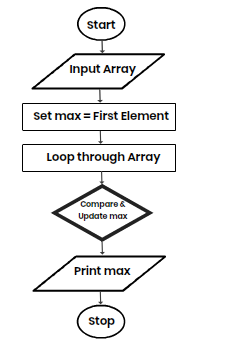
Example Flowchart (Find the Largest Number in an Array):
- Start → Oval (Represents Start)
- Input Array → Parallelogram (Represents Input)
- Set max = First Element → Rectangle (Represents Processing)
- Loop through Array → Rectangle (Represents Processing)
- Compare & Update max → Diamond (Represents Decision-making, checking if the current element is greater than max)
- Print max → Parallelogram (Represents Output)
- Stop → Oval (Represents Stop)
Conclusion
✅ Algorithms provide structured steps for problem-solving.
✅ Pseudocode helps in designing logic before actual coding.
✅ Flowcharts offer a visual representation of program flow.
By combining these techniques, programmers can efficiently solve problems and develop optimized solutions.

These notes are easy to understand. Thanks